【注意】算法系列已经重新整理到github中，不在博客中继续更新了。

基础概念

首先，哈希表 是根据关键码进行直接访问的数据结构，一个数组也可以是一个哈希表，索引下标为关键码，数组中的元素为值。

哈希表能够处理的问题：快速判断（O(1)）一个元素是否出现在集合中【牺牲空间换取时间】。

哈希函数

如下图所示，哈希函数将学生姓名转化为数值，就成功将学生名字（string）映射成哈希表上的索引数字了。

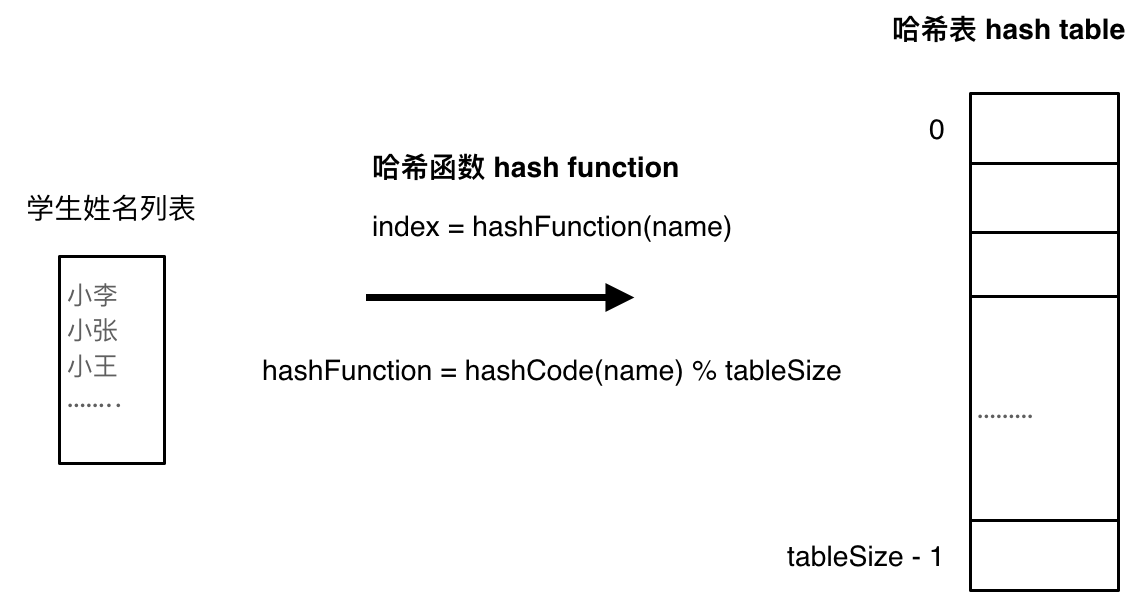
为防止hashCode计算得到的值大于哈希表的大小，需要一个取模的运算，保证所有得到的索引都落在哈希表的范围中。

但是这样，又会产生新的问题，即会存在有多个不同学生的名字同时映射到哈希表中的同一个位置上。

哈希碰撞

上述问题，就被称为哈希碰撞。解决碰撞有很多种方式，这里说常见的两种：拉链法 和 线性探测法。

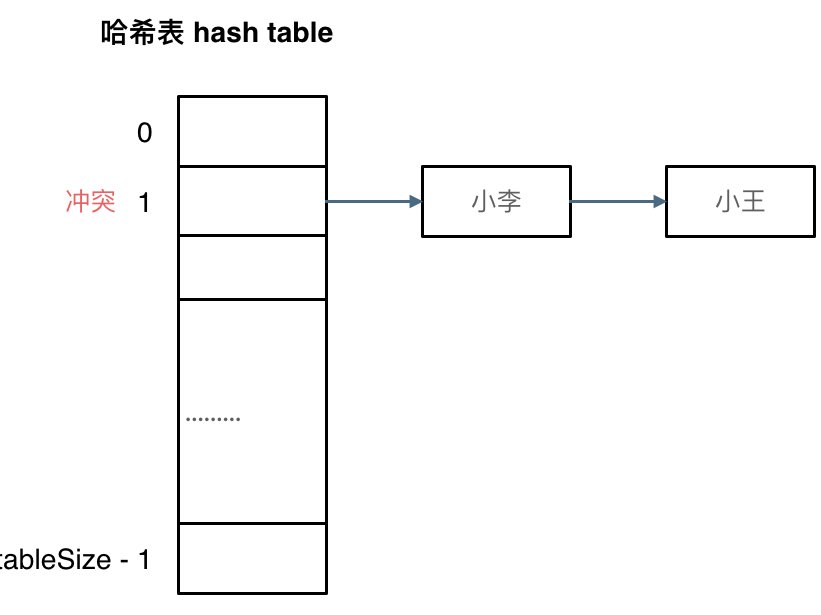
拉链法：哈希表中元素为链表，冲突元素的下标相同，放在同一个链表中。

))

拉链法要选择适当的哈希表大小，这样既不会因为数组空闲而浪费内存，也不会因为链表太长而在查找上浪费时间。

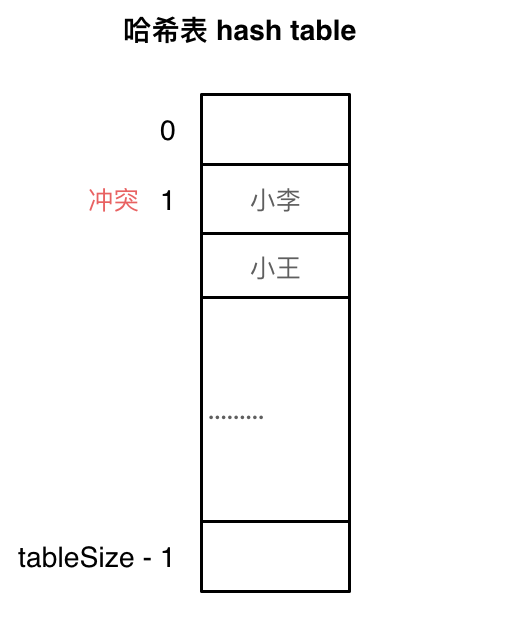
线性探测法：依靠哈希表中的空位解决碰撞问题，要保证 哈希表的大小 大于 数据量。

具体方法就是，如果这个索引位置被占用了，就找下一个空位。

常见的三种哈希结构

一般用哈希表解决问题时，会选择如下三种数据结构来表示哈希表：

• 数组
• set（集合）
• map（映射表）

c++中，提供了不同的set和map实现，其底层实现和优劣总结在下表中：

集合	底层实现	key是否有序	key是否重复	key是否可修改	查询效率	增删效率
std::set	红黑树	有序	否	否	O(log n)	O(log n)
std::multiset	红黑树	有序	是	否	O(log n)	O(log n)
std:unordered_set	哈希表	无序	否	否	O(1)	O(1)

说明：红黑树是一种平衡二叉树，所以key值有序，但是不能修改，否则会导致整棵树的错乱，所以只能增加或删除。

映射表	底层实现	key是否有序	key是否重复	key是否可修改	查询效率	增删效率
std::map	红黑树	有序	否	否	O(log n)	O(log n)
std::multimap	红黑树	有序	是	否	O(log n)	O(log n)
std::unordered_map	哈希表	无序	否	否	O(1）	O(1)